直角三角形斜边上的中线等于斜边的一半证明,直角三角形斜边上的中线等于斜边
直角三角形斜边上的中线等于斜边的一半证明,直角三角形斜边上的中线等于斜边的一半怎么证
斜边上的中线等于斜边的一半证明了这一点。但是,如果我们假设一个三角形的顶点是正方形的底点,那么这个三角形的顶点就是正方形的底点。因此,我们可以得到一个结结论:如果我们想知道三角形的底点是什么,我们就必须知道三角形的顶点是什么。这就是为什么我们需要用正方形的底点来代替三角形的顶点的因。在这个例子中,我们可以看到三角形的底点是一个正方形的底点,而三角形的顶点是一个正方形的顶点。
一:直角三角形斜边上的中线等于斜边的一半证明
证明过程如下:
取AC的中点E,连接DE。取BC的中点D
∵AD是斜边BC的中线
∴BD=CD=1/2BC
∵E是AC的中点
∴DE是△ABC的中位线
∴DE//AB(三角形的中位线平行于底边)
∴∠DEC=∠BAC=90°(两直线平行,同位角相等)
∴DE垂直平分AC
∴AD=CD=1/2BC(垂直平分线上的点到线段两端距离相等)
直角三角形的性质:
1、直角三角形中,斜边上的中线等于斜边的一半(也就是直角三角形的外心位于斜边的中点,外接圆半径R=C/2)。
2、在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半。在直角三角形中,如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°。
简单计算一下,答案如图所示
二:直角三角形斜边上的中线等于斜边的一半吗
因为这是直角三角形的一种属性,是可以证明的。证法:设三角形的两条直角边为a、b,斜边为c,中线为d。a²+b²=c²,且d为斜边的中线,所以对同一个角B,a²-1/2c²+b²=2d²,a²+b²=c²,代入得:1/2c²=2d2,d1=1/2c,d2=-1/2c(舍)所以 d=1/2c,命题得证。
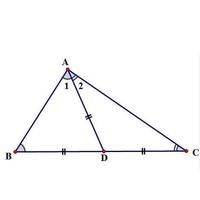
其逆命题:如果一个三角形的一条边的中线等于这条边的一半,那么这个三角形就是直角三角形,而且这条边为直角三角形的斜边。
所以逆命题是正确的。以该条边的中点为圆心,以中线长为半径作圆,则该条边成为圆的直径,该三角形的另一个顶点在圆上,该顶角为圆周角。因为直径上的圆周角是直角,所以逆命题1成立。
三:直角三角形斜边上的中线等于斜边的一半什么时候学的
对于给出中点时,部分同学对中位线、中线掌握不到位,遇到题目中有直角三角形斜边上的中点,经常视而不见,从而想不到斜边中线处理线段之间数量关系时的妙用;而有时出现多个中点,想不到再找中点,从而也就看不见隐藏的中位线了,本讲就精选几道例题帮助同学们突破难点.
一、想不到的斜边中线
例1:
如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=8,则EF的长为________.
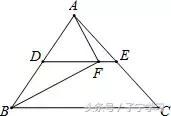
分析:
根据DE是中位线,可知DE长是第三边BC长的一半,点D是AB的中点.由∠AFB=90°,则Rt△ABF中,可知DF作为斜边中线,长度等于斜边AB长的一半,将DE的长减去DF的长,即可得到EF的长.
解答:
例2:
如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.
分析:
(1)根据三角形的中位线平行于第三边并且等于第三边的一半,可得DE∥AC,EF∥AB,两组对边分别平行的四边形是平行四边形.
(2)D,F分别作为Rt△ABH,Rt△ACH斜边AB,AC上的中线,根据直角三角形斜边上的中线等于斜边的一半,可得DH=AD,FH=AF,∠BAH=∠AHD,∠CAH=∠AHF,即∠BAC=∠DHF,由平行四边形对角相等可得∠DEF=∠BAC,等量代换即可得证.
解答:
证明:
(1)∵点D,E,F分别是AB,BC,CA的中点,
∴DE、EF是△ABC的中位线,
∴DE∥AC,EF∥AB,
∴四边形ADEF是平行四边形.
(2)∵AH是边BC上的高,D,F分别是AB,CA中点
∴Rt△ABH中,DH=AD,Rt△ACH中,FH=AF,
∴∠BAH=∠AHD,∠CAH=∠AHF,
∴∠DHF=∠BAC,
∵四边形ADEF是平行四边形,
∴∠DEF=∠BAC,
∴∠DHF=∠DEF.
本题也可连接DF,证明△DEF≌△FHD
小结:
许多题目中,会出现多个中点,有的中点与另一中点相连,作为中位线;而有的中点与直角顶点相连,就成了斜边中线,而这都涉及到线段长度之间的倍数关系,尤其是后者,不能忽视.
二、看不见的中位线
(1)补全三角形
例1:
在△ABC中,CD平分∠ACB,AD⊥CD于D,E是AB中点,AC=15,BC=27,求DE的长.
分析:
本题中,点E已经是AB的中点,由CD平分∠ACB,AD⊥CD,想到可以构造等腰三角形,利用三线合一,使点D成为另一个中点,从而让ED变成“看得见”的中位线.
解答:
例2:
如图△ABC中,∠B,∠C的平分线BE,CF相交于O,AG⊥BE于G,AH⊥CF于H.
(1)求证:GH∥BC;
(2)若AB=9,AC=14,BC=18,求GH.
(3)若将条件“∠B,∠C的平分线”改为“∠B的平分线及∠C的外角平分线”(如图2所示),或改为“∠B,∠C的外角平分线”(如图3所示),其余条件不变,求证:结论GH∥BC仍成立.
分析:
与上例类似,有角平分线,有垂直,延长构造等腰三角形,利用三线合一.
解答:
(1)证明:
分别延长AG,AH交BC于M,N,
在△ABM中
∵BG平分∠ABM,BG⊥AM,
∴∠ABG=∠MBG,∠BGA=∠BGM=90°
∴∠BAM=∠BMA.
∴BA=BM,G是AM的中点.
同理CA=CN,H是AN的中点,
∴GH是△AMN的中位线,HG∥MN,HG∥BC.
(2)
由(1)知,△ABG≌△MBG,△ACH≌△NCH,
∴AB=BM=9,AC=CN=14.
∴MN=BM+CN-BC
=AB+AC-BC=9+14-18=5
(3)无字证明如下,相信同学们都能看懂.
(2)找边的中点
例1:
分析:
根据要证明的结论,我们可以发现这与三角形三边关系有关,因此,要构造一个以CD长的一半,AB长的一半,EF长为三边的三角形,自然想到中位线,取BC边的中点即可.
解答:
变式:
已知在四边形ABCD中,AC=BD,E、F分别是AB、DC的中点.求证:OM=ON.
分析:
要证OM=ON,可以从等角对等边入手,证∠OMN=∠ONM,考虑到对角线AC=BD,能不能再来一次等边对等角呢?构造AC,BD的一半即可,则需要构造中位线,自然想到BC的中点.
解答:
(3)找对角线的中点
例1:
如图,四边形ABCD中,E为AD中点,F为BC中点.求证:AB+CD>2EF.
分析:
根据要证明的结论,,似乎又与三角形三边关系有关,将不等式两边同除以2,则只需构造以EF,AB长的一半,DC长的一半为边的三角形,想到连接对角线取中点.
解答:
变式:
如图,在四边形ABCD中,AD=BC,E、F分别是DC、AB边的中点,FE的延长线分别与AD、BC的延长线交于H、G点.求证:∠AHF=∠BGF.
分析:
与例1的变式类似,要借助其他两个相等的角转化,考虑到对边相等,则构造AD,BC的一半即可,则需要构造中位线,自然想到对角线AC的中点.
解答:
小结:
对于以上4题,我们都需要找中点,构造中位线,但 *** 各异,有取四边形边的中点,有取四边形对角线的中点,能否找到一些规律呢?其实不难!
例1,例2,最后证明的结论都与一组对边有关.
例1,要证明的一组对边必作为第三边,已经给出对角线的中点,那么必然要再取另一对边中的一条的中点.
例2,要证明的一组对边必作为第三边,已经给出另一组对边的中点,,那么必然再取一条对角线的中点.
例1的变式,例2的变式,最后要证明的结论都是角等,也就是边等.
例1的变式中,对角线相等,必作为第三边,给出一对边的中点,那么必然再取另一组对边中的一条的中点.
例2的变式中,一组对边相等,必作为第三边,给出另一组对边的中点,那么必然再取一条对角线的中点.
由此可见,关键在于选择谁作第三边.
有些结论比较明显的,直接以结论中涉及的边为第三边,
对于不明显的,则需要转换,但一般如果题目中有两条线段相等的条件,则这两条相等的线段必然作第三边.
本讲思考题3例
1、如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF=________.
2、如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上移动,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为________.
3、如图,在△ABC中,若∠B=2∠C,AD⊥BC,E为BC边中点,求证:AB=2DE.
-

- 洗洁精洗会影响眼镜镀膜,洗洁精会把眼镜镀膜洗掉吗
-
2023-09-24 18:03:26
-

- 天然气有味道吗,家用做饭的天然气有味吗?
-
2023-09-24 18:01:17
-
- 燃气灶火焰小是怎么回事,燃气灶火小的原因是什么,要怎么办?
-
2023-09-24 17:59:10
-

- 全球气候变暖的影响,全球气候变暖对发展中国家的经济的影响?
-
2023-09-24 17:57:04
-

- 男女朋友之间的称呼,男女朋友之间的互称叫什么?
-
2023-09-24 17:54:59
-

- 老鼠怕水吗,老鼠怕水的吗?
-
2023-09-24 17:52:53
-

- 考试加油鼓励的短句,期末考试加油鼓励的句子小学老师?
-
2023-09-24 17:50:46
-

- 开车是什么意思,请问网上说得“开车”是什么意思?总是说老司机带我之类的话
-
2023-09-24 17:48:41
-

- 金山寺在哪,镇江金山寺在市中心吗?
-
2023-09-24 17:46:35
-

- 动车晚点么,动车晚点是什么意思?
-
2023-09-24 17:44:29
-
- 辰在名字里的寓意,辰字取名含义是什么意思
-
2023-09-24 17:36:28
-

- 不撞南墙不回头是什么意思,不撞南墙不回头,槛外长江空自流什么意思?
-
2023-09-24 17:34:22
-

- 保健食品经营许可,保健食品经营许可有效期?
-
2023-09-24 17:32:17
-

- 白凉粉是啥,白凉粉是什么植物里面提炼出来的?
-
2023-09-24 17:30:10
-

- 熬粥要多长时间,小火熬粥要多长时间
-
2023-09-24 17:28:05
-

- agoni是什么意思,Agoni英文是什么意思?中文怎么发音?
-
2023-09-24 17:25:58
-
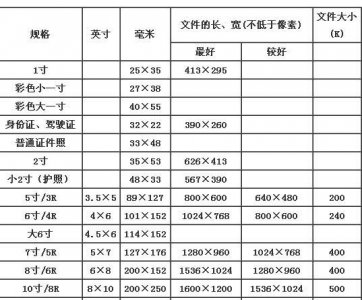
- 2寸照片尺寸,2寸照片的尺寸是多少厘米?
-
2023-09-24 17:23:52
-

- c开头的火车是什么车,c开头是什么车是火车还是动车
-
2023-09-24 04:26:20
-

- 驱逐舰与护卫舰的区别,怎样肉眼区分驱逐舰与护卫舰
-
2023-09-24 04:24:15
-
- 大湾区包括哪些城市,上海大湾区包括哪些城市?
-
2023-09-24 04:22:10



 什么是领域驱动设计(领域驱动设计中的相关核心概念)
什么是领域驱动设计(领域驱动设计中的相关核心概念) onlylove歌词什么意思(onlylove歌词含义)
onlylove歌词什么意思(onlylove歌词含义)